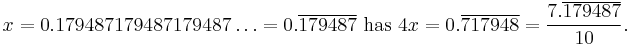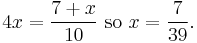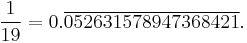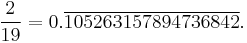Parasitic number
An n-parasitic number (in base 10) is a positive natural number which can be multiplied by n by moving the rightmost digit of its decimal representation to the front. Here n is itself a single-digit positive natural number. In other words, the decimal representation undergoes a right circular shift by one place. For example, 4•128205=512820, so 128205 is 4-parasitic. Most authors do not allow leading zeros to be used, and this article follows that convention. So even though 4•025641=102564, the number 025641 is not 4-parasitic.
Contents |
Derivation
An n-parasitic number can be derived by starting with a digit k (which should be equal to n or greater) in the rightmost (units) place, and working up one digit at a time. For example, for n = 4 and k = 7:
- 4•7=28
- 4•87=348
- 4•487=1948
- 4•9487=37948
- 4•79487=317948
- 4•179487=717948.
So 179487 is a 4-parasitic number with units digit 7. Others are 179487179487, 179487179487179487 etc.
Notice that the repeating decimal
Thus
In general, an n-parasitic number can be found as follows. Pick a one digit integer k such that k ≥ n, and take the period of the repeating decimal k/(10n−1). This will be 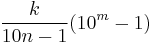 where m is the length of the period; i.e. the order of 10 modulo (10n − 1).
where m is the length of the period; i.e. the order of 10 modulo (10n − 1).
For another example, if n = 2, then 10n − 1 = 19 and the repeating decimal for 1/19 is
So that for 2/19 is double that:
The length m of this period is 18, the same as the order of 10 modulo 19, so 2 × (1018 − 1)/19 = 105263157894736842.
105263157894736842 × 2 = 210526315789473684, which is the result of moving the last digit of 105263157894736842 to the front.
Smallest n-parasitic numbers
The smallest n-parasitic numbers are also known as Dyson numbers, after a puzzle concerning these numbers posed by Freeman Dyson.[1][2][3] They are:
| n | Smallest n-parasitic number | period of |
| 1 | 1 | 1/9 |
| 2 | 105263157894736842 | 2/19 |
| 3 | 1034482758620689655172413793 | 3/29 |
| 4 | 102564 | 4/39 |
| 5 | 142857 | 7/49=1/7 |
| 6 | 10169491525423728813559932203389830508474576271186440677966 | 6/59 |
| 7 | 1014492753623188405797 | 7/69 |
| 8 | 1012658227848 | 8/79 |
| 9 | 10112359550561797752808988764044943820224719 | 9/89 |
General note
In general, if we relax the rules to allow a leading zero, then there are 9 n-parasitic numbers for each n. Otherwise only if k ≥ n then the numbers do not start with zero and hence fit the actual definition.
Other n-parasitic integers can be built by concatenation. For example, since 179487 is a 4-parasitic number, so are 179487179487, 179487179487179487 etc.
See also
Notes
- ^ Dawidoff, Nicholas (March 25, 2009), "The Civil Heretic", New York Times Magazine, http://www.nytimes.com/2009/03/29/magazine/29Dyson-t.html.
- ^ Tierney, John (April 6, 2009), "Freeman Dyson’s 4th-Grade Math Puzzle", New York Times, http://tierneylab.blogs.nytimes.com/2009/04/06/freeman-dysons-4th-grade-math-puzzle/.
- ^ Tierney, John (April 13, 2009), "Prize for Dyson Puzzle", New York Times, http://tierneylab.blogs.nytimes.com/2009/04/13/prize-for-dyson-puzzle/.
References
- C. A. Pickover, Wonders of Numbers, Chapter 28, Oxford University Press UK, 2000.
- Sequence A092697 in the On-Line Encyclopedia of Integer Sequences.